Все калькуляторы
Ортоцентр — точка пересечения высот треугольника
Чтобы найти ортоцентр треугольника, можно воспользоваться калькулятором, где следует внести координаты. В автоматическом режиме с помощью формул произведется расчет. Можно также все расчеты произвести самостоятельно.
Например, имеются следующие данные точек:
А – 4,3;
В – 0,5;
С – 3,-6.
Первое , что необходимо найти наклон сторон, который обозначается - m , используется формула :
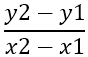
Из этого следует:
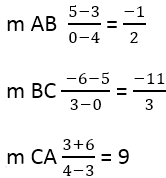
Далее необходимо найти наклон перпендикулярных сторон, для этого используется формула:
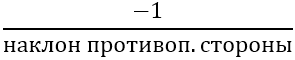
Имеем:
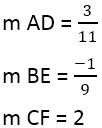 Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:
Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:
С помощью упрощения, имеем: 3х - 11у=-21
Для линии ВЕ, где точка 0,5, а наклон -1/9, имеем 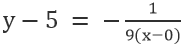
Упрощение дает: х+9у=45.
И последние линии CF, где точка 3, -6, а наклон 2, имеем уравнение y+6 = 2(x-3).
И упрощение, 2x — y = 12.
Если решить два из трех уравнений будут найдены значения х и у. Для данного примера:
Значение х = 8,05263;
Значение у = 4,10526.
Которые в данном случае являются координатами искомого Ортоцентра.
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.