Все калькуляторы
Диагональ куба
Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба - трех его измерений одинаковых измерений) названа в его честь.
Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.
Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).
Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле: d=a√2
Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:
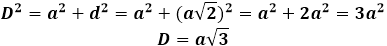
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.